Der Begriff "scaenographia"
taucht bei Vitruv im zweiten Kapitel des ersten Buchs an der Stelle auf,
wo er "die ästhetischen Begriffe der Baukunst"
erläutert.
Die Formen der Dispositio sind folgende; "Ichnographia,
Orthographia, Scaenographia". Vereinfacht ausgedrückt bezeichnet
er damit Grundriss, Aufriss und "die illusionistische
Wiedergabe der Fassade und der zurücktretenden Seiten".
In der Vorrede zum 7.Buch, in der er seine literarischen Quellen rühmt,
erwähnt er den Agatharchos von Samos als Verfasser einer Schrift über
Bühnenmalerei, in der es im wesentlichen darum geht körperhafte
Dinge auf senkrechten und ebenen Oberflächen so zu malen, dass "das
eine zurücktretend, anderes hervortretend zu sein scheint".
Die Szenographie wird schon vom Wort her ursprünglich mit der
Bühnen- und Kulissenmalerei in Verbindung gebracht und viel mehr als
das hier zitierte ist aus Vitruv darüber auch nicht zu erfahren. Ob
es sich dabei um eine der Perspektive verwandte Methode gehandelt hat,
muss man annehmen. Panofsky spekuliert über ein Verfahren, das er
im Gegensatz zur planperspektivischen Zentralperspektive ein winkelperspektivisches
nennt, demzufolge die Sehgrößen nicht durch die Entfernung der
Objekte von Auge bestimmt sind, sondern durch das Maß der Sehwinkel.
(Panofsky,
Perspektive als symbolische Form S.104)
 |
Nach einem winkelperspektivischen Verfahren
müsste die Projektion von Gegenständen auf eine "Seh-Kugel"
erfolgen und wären Geraden stets als Kurven abzubilden damit
sie als gerade empfunden werden können. Warum diese auf Euklid
zurückgeführten und ansich klugen Überlegungen nicht zur
Entwicklung kugelförmig gewölbter Bildflächen bei den Griechen
geführt haben, erklärt Panofsky nicht. Mit Ausnahme der Vasenmalerei
haben die Griechen in der Hauptsache auf Holztafeln und auf ebene Wände
gemalt. Bei der Übertragung winkelperspektivischer Gesetzmäßigkeiten
auf ebene Bildflächen "erhält man jedenfalls
(für die Darstellung eines Raumkastens)
ein Resultat, das mit den erhaltenen Denkmälern in einer entscheidenden
Tatsache übereinstimmt: die Verlängerung der Tiefenlinien laufen
nicht...in einem Punkte zusammen, sondern sie treffen sich nur leise konvergierend,
paarweise in mehreren Punkten, die alle auf einer gemeinsamen Achse liegen."
Diese
Achse nennt er Fluchtachse, und derlei Fluchtachsen kann Panofsky
in zahlreichen Bildern nachweisen.
Meister Bertram; Geburt
Christi; 1340-1414/15; Grabower Altar; 85x57 cm, Eichenholz;
Panofsky kennt zwei Lesarten des Begriffs
Scenografie: sie ist "1. die Methode des
Malers, der Gebäude darstellen will und dabei nicht ihre wahren, sondern
ihre scheinbaren Maße zur Wiedergabe bringen muß, 2. die Methode
des Architekten, der nicht die unter abstrakt mathematischen Gesichtspunkten
schönen Proportionen anwenden darf..."sondern..."den Täuschungen
des Auges entgegenarbeiten muss, 3. die Methode des Großplastikers,
den die Skenographie über den künftigen optischen Eindruck seines
Kunstwerks belehrt..." |
Die einzigen überlieferten Wandgemälde
der Antike nach dieser Methode stammen laut Sellenriek aus hellenistischer
Zeit und liegen auf römischem Boden (z.B. Villa Livia, Rom).
 „Nach
allem, was man dort ablesen kann, können damals die Gesetzmäßigkeiten
der Perspektive in ihrem ganzen Umfang noch nicht begriffen gewesen sein.
Gleichwohl liegt es im Bereich der Wahrscheinlichkeit, dass es den antiken
Skenographen mit ihrem für visuell-optische Phänomene geschulten
Blick nicht entgangen ist, wie das sogenannte Fluchten von Parallelen,
ihr Zusammenstreben auf einen imaginären Punkt, dann nicht mehr wahrnehmbar
ist wenn die angeschauten Dinge in Bezug zur Größe des Betrachters
entweder sehr klein oder sehr weit entfernt sind, d.h. ihre Parallelen
auch im Bild annähernd parallel erscheinen müssen. Schaut man
z.B. eine Zündholzschachtel aus mehr als einem Meter Entfernung an,
so bleiben auch ihre Parallelkanten für die Wahrnehmung parallel,
ganz im Gegensatz zu denen eines Gebäudes aus >normaler Distanz<.
Theoretisch geht die Fluchtpunktperspektive bei einem unendlich großen
Abbildungsabstand, praktisch aber schon, wenn dieser ein erhebliches Vielfaches
der Gegenstandsgröße ausmacht, in die Parallelperspektive über,
in der eben Parallelität erhalten bleibt.“(Sellenriek
S. 58) „Nach
allem, was man dort ablesen kann, können damals die Gesetzmäßigkeiten
der Perspektive in ihrem ganzen Umfang noch nicht begriffen gewesen sein.
Gleichwohl liegt es im Bereich der Wahrscheinlichkeit, dass es den antiken
Skenographen mit ihrem für visuell-optische Phänomene geschulten
Blick nicht entgangen ist, wie das sogenannte Fluchten von Parallelen,
ihr Zusammenstreben auf einen imaginären Punkt, dann nicht mehr wahrnehmbar
ist wenn die angeschauten Dinge in Bezug zur Größe des Betrachters
entweder sehr klein oder sehr weit entfernt sind, d.h. ihre Parallelen
auch im Bild annähernd parallel erscheinen müssen. Schaut man
z.B. eine Zündholzschachtel aus mehr als einem Meter Entfernung an,
so bleiben auch ihre Parallelkanten für die Wahrnehmung parallel,
ganz im Gegensatz zu denen eines Gebäudes aus >normaler Distanz<.
Theoretisch geht die Fluchtpunktperspektive bei einem unendlich großen
Abbildungsabstand, praktisch aber schon, wenn dieser ein erhebliches Vielfaches
der Gegenstandsgröße ausmacht, in die Parallelperspektive über,
in der eben Parallelität erhalten bleibt.“(Sellenriek
S. 58)
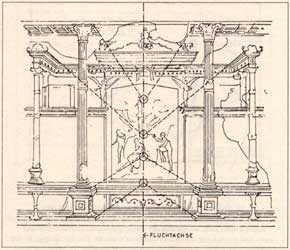
Die Abbildung zeigt eine
Rekonstruktion von J. Harvest der Fluchtachsenperspektive eines Wandgemäldes
aus der Villa Livia auf dem Palatin in Rom, 1. Jh v. Chr. Abb. aus Sellenriek
S.131 |
Für den Plattenboden des Meister Bertram
liefert das Verfahnen offensichtlich keine optisch überzeugende Rezeptur.
So haben denn auch die Maler des 15. Jh. im Norden wie im Süden für
diesen Spezialfall bald der Lösung mit konvergierenden Fluchtlinien
den Vorzug gegeben, wobei etwa noch im Umfeld von van Eyck für die
Orthogonalen des Plattenbodens und die des Deckengebälks getrennte
Fluchtpunkte unter Beibehaltung der vertikalen Fluchtachse üblich
waren. |
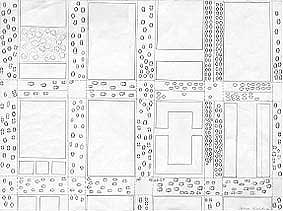
 Landkartenbild
und Standlinienbild werden in der Literatur der Kinderzeichnung
(z.B. bei H.G. Richter) als Bildformen in der Schemaphase beschrieben.
Als Bildsorten eines beschreibenden Bildkonzepts kann man das Landkartenbild
mit dem Grundriss und das Standlinienbild mit dem Aufriss
vergleichen. Als Bildschemata geben sie nicht in erster Linie einen Gesichtseindruck
wieder sondern bedeuten eine Symbolisierung. So symbolisiert das Landkartenbild
eine Bewegung im Raum gleichsam als Durchschreiten einer Landschaft, bei
dem die Lage der Bildobjekte zueinander als Abstände erfahren werden,
während das Standlinienbild durch eine Nebeneinanderreihung der Bildobjekte
die charakteristischen Objektansichten symbolisiert, in der Regel ohne
Berücksichtigung ihrer Lage und Staffelung im Raum. In der reinen
Form sind beide in der Kinderzeichnung eher selten. Oft finden sich beide
Formen vermischt, wie etwa in der Darstellung des Schulwegs durch eine
10jährige Schülerin, die Aufsicht und Ansicht in alterstypischer
Weise kombiniert.
Landkartenbild
und Standlinienbild werden in der Literatur der Kinderzeichnung
(z.B. bei H.G. Richter) als Bildformen in der Schemaphase beschrieben.
Als Bildsorten eines beschreibenden Bildkonzepts kann man das Landkartenbild
mit dem Grundriss und das Standlinienbild mit dem Aufriss
vergleichen. Als Bildschemata geben sie nicht in erster Linie einen Gesichtseindruck
wieder sondern bedeuten eine Symbolisierung. So symbolisiert das Landkartenbild
eine Bewegung im Raum gleichsam als Durchschreiten einer Landschaft, bei
dem die Lage der Bildobjekte zueinander als Abstände erfahren werden,
während das Standlinienbild durch eine Nebeneinanderreihung der Bildobjekte
die charakteristischen Objektansichten symbolisiert, in der Regel ohne
Berücksichtigung ihrer Lage und Staffelung im Raum. In der reinen
Form sind beide in der Kinderzeichnung eher selten. Oft finden sich beide
Formen vermischt, wie etwa in der Darstellung des Schulwegs durch eine
10jährige Schülerin, die Aufsicht und Ansicht in alterstypischer
Weise kombiniert.
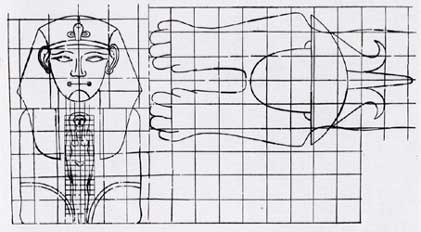 „Grundriss“
und „Aufriss“ in diesem allgemeinen Sinn kommen als Darstellungsformen
bereits 2000 Jahre vor Christus bei den Ägyptern vor, bei Architekturdarstellungen
und in der Bildhauerei sogar im Zusammenhang, wobei dem Grundriss durch
Umklappen an einer Linie des üblichen Quadratrasters ein Aufriss bereits
maßstäblich zugeordnet sein kann (Sellenriek,
„Zirkel und Lineal“, S. 32). Vitruv erwähnt im 1. Jh. vor Chr.
zwei von den Griechen übernommene Darstellungsarten, die „ichnographia“
und die „orthographia“. Der erste Begriff bedeutet so viel wie „Fußspurzeichnung“
und der zweite „Aufrechtzeichnung“ (Sellenriek S.41).
Sellenriek verneint allerdings für die Ägypter den Zusammenhang
dieser räumlichen Zuordnung mit einem optischen Projektionsmodell,
wie es etwa bereits die Erfahrung von Schattenrissen hätte liefern
können. Die rechte Darstellung liefert die Rekonstruktion einer ägyptischen
Zeichnung auf einem Papyrusblatt aus dem 3. Jh. v.Chr., das in Berlin aufbewahrt
wird. (nach H. Schäfer, "Von Ägyptischer Kunst").
Für das Standlinienbild gibt es bereits bei
den Griechen ein interessante Bezeichnung, die "Isokephalie", was
soviel bedeutet wie "auf gleicher Kopfhöhe".
„Grundriss“
und „Aufriss“ in diesem allgemeinen Sinn kommen als Darstellungsformen
bereits 2000 Jahre vor Christus bei den Ägyptern vor, bei Architekturdarstellungen
und in der Bildhauerei sogar im Zusammenhang, wobei dem Grundriss durch
Umklappen an einer Linie des üblichen Quadratrasters ein Aufriss bereits
maßstäblich zugeordnet sein kann (Sellenriek,
„Zirkel und Lineal“, S. 32). Vitruv erwähnt im 1. Jh. vor Chr.
zwei von den Griechen übernommene Darstellungsarten, die „ichnographia“
und die „orthographia“. Der erste Begriff bedeutet so viel wie „Fußspurzeichnung“
und der zweite „Aufrechtzeichnung“ (Sellenriek S.41).
Sellenriek verneint allerdings für die Ägypter den Zusammenhang
dieser räumlichen Zuordnung mit einem optischen Projektionsmodell,
wie es etwa bereits die Erfahrung von Schattenrissen hätte liefern
können. Die rechte Darstellung liefert die Rekonstruktion einer ägyptischen
Zeichnung auf einem Papyrusblatt aus dem 3. Jh. v.Chr., das in Berlin aufbewahrt
wird. (nach H. Schäfer, "Von Ägyptischer Kunst").
Für das Standlinienbild gibt es bereits bei
den Griechen ein interessante Bezeichnung, die "Isokephalie", was
soviel bedeutet wie "auf gleicher Kopfhöhe".
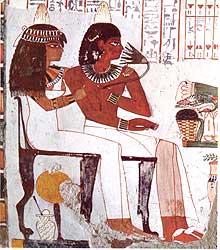
 Bei
der ägyptischen Zeichnung und Malerei ist der Zusammenhang von Bild
und Text augenscheinlich. So haben bildhafte Symbole nicht nur den Text
illustrativ begleitet sondern auch direkten Eingang in die Bilderschrift
der Hieroglyphen gefunden. Bei Carl Schuchhardt, ("Die Burg
im Wandel der Weltgeschichte", Wiesbaden 1991 S.3) stosse ich auf
die Beschreibung von Hieroglyphenzeichen, die "so alt wie die ägyptische
Schrift selbst" sind und ein Symbol für die Burg, Befestigung darstellen
und Türme oder ummauerte Anlagen in Grundriss wie im Aufriss zeigen.
Bei
der ägyptischen Zeichnung und Malerei ist der Zusammenhang von Bild
und Text augenscheinlich. So haben bildhafte Symbole nicht nur den Text
illustrativ begleitet sondern auch direkten Eingang in die Bilderschrift
der Hieroglyphen gefunden. Bei Carl Schuchhardt, ("Die Burg
im Wandel der Weltgeschichte", Wiesbaden 1991 S.3) stosse ich auf
die Beschreibung von Hieroglyphenzeichen, die "so alt wie die ägyptische
Schrift selbst" sind und ein Symbol für die Burg, Befestigung darstellen
und Türme oder ummauerte Anlagen in Grundriss wie im Aufriss zeigen.
 Mir
fällt beim Stichwort „Schattenprojektion“ ein, dass Schüler
gelegentlich beim Zeichnen räumlicher Buchstaben vom „Schatten“ sprechen,
wie das im übrigen auch Grafik- oder Layout-Programme tun. So ein
Schatten erzeugt zwar einen räumlichen Effekt durch seitlich verschobene
Überlagerung zweier gleichförmiger Figuren, von denen man eine
als vorn, die andere als hinten liest. Ein Raumbild eines Buchstaben jedoch
würde anders aussehen müssen, wie auch der parallel projizierte,
unverzerrte Schatten nur eine Möglichkeit der Schattenbildung
darstellt. Schattenprojektionen führen zu Verzerrungen wenn die Projektionsfläche
nicht parallel zur Hauptebene des projizierten Objekts liegt oder wenn
die Projektionsstrahlen nicht parallel sind, wie etwa bei punktförmigen
Lichtquellen. Sonnenlicht und eine zum Objekt parallel liegende Projektionsfläche
können jedoch auch zu annähernd unverzerrten Schattenfiguren
führen weil das Sonnenlicht das Grundmodell für eine Parallelprojektion
liefert.
Mir
fällt beim Stichwort „Schattenprojektion“ ein, dass Schüler
gelegentlich beim Zeichnen räumlicher Buchstaben vom „Schatten“ sprechen,
wie das im übrigen auch Grafik- oder Layout-Programme tun. So ein
Schatten erzeugt zwar einen räumlichen Effekt durch seitlich verschobene
Überlagerung zweier gleichförmiger Figuren, von denen man eine
als vorn, die andere als hinten liest. Ein Raumbild eines Buchstaben jedoch
würde anders aussehen müssen, wie auch der parallel projizierte,
unverzerrte Schatten nur eine Möglichkeit der Schattenbildung
darstellt. Schattenprojektionen führen zu Verzerrungen wenn die Projektionsfläche
nicht parallel zur Hauptebene des projizierten Objekts liegt oder wenn
die Projektionsstrahlen nicht parallel sind, wie etwa bei punktförmigen
Lichtquellen. Sonnenlicht und eine zum Objekt parallel liegende Projektionsfläche
können jedoch auch zu annähernd unverzerrten Schattenfiguren
führen weil das Sonnenlicht das Grundmodell für eine Parallelprojektion
liefert.
 Eine
ganze Reihe von Aufgaben lassen sich finden als Anwendung sowohl des "Fußspurzeichnens"
als auch der Parallelprojektion nach Regeln der Kavaliers- oder
der Militärperspektive. Es ist nur sinnvoll und didaktisch
klug, derartige Aufgaben zunächst mit der flächigen Darstellung
des Grundrisses zu beginnen und danach "wie der Maurer" die Wände
hochzuziehen. Für solche Zwecke habe ich ein kariertes Papier so stark
hochkopiert, dass die Rasterquadrate 1cm Kantenlänge erhalten. Das
lässt sich als Zeichenhilfe unter das Arbeitsblatt legen und scheint
dann noch ausreichend deutlich durch. Die Quadratdiagonale gibt den Winkel
von 45 Grad vor. Ein nachträgliches Bezeichnen der drei Raumrichtungen
mit drei Tönen klärt die räumliche Lesbarkeit. Im Gegensatz
zur Zentralprojektion liefert die Paralellprojektion neben dem 3-Tafel-System
in den diversen Parallelperspektiven einfache und überschaubare Regelsysteme,
mit denen sich vielfältige beschreibende Aufgaben sehr klar lesbar
lösen lassen: Isometrie, Dimetrie, Kavaliersperspektive
und Militärperspektive gehen zurück auf die Bemühungen barocker
Ingenierskunst, eindeutige Darstellungsverfahren für konstruktive
Aufgaben zu schaffen (Desargues "Brouillon project" 1636-40).
Eine
ganze Reihe von Aufgaben lassen sich finden als Anwendung sowohl des "Fußspurzeichnens"
als auch der Parallelprojektion nach Regeln der Kavaliers- oder
der Militärperspektive. Es ist nur sinnvoll und didaktisch
klug, derartige Aufgaben zunächst mit der flächigen Darstellung
des Grundrisses zu beginnen und danach "wie der Maurer" die Wände
hochzuziehen. Für solche Zwecke habe ich ein kariertes Papier so stark
hochkopiert, dass die Rasterquadrate 1cm Kantenlänge erhalten. Das
lässt sich als Zeichenhilfe unter das Arbeitsblatt legen und scheint
dann noch ausreichend deutlich durch. Die Quadratdiagonale gibt den Winkel
von 45 Grad vor. Ein nachträgliches Bezeichnen der drei Raumrichtungen
mit drei Tönen klärt die räumliche Lesbarkeit. Im Gegensatz
zur Zentralprojektion liefert die Paralellprojektion neben dem 3-Tafel-System
in den diversen Parallelperspektiven einfache und überschaubare Regelsysteme,
mit denen sich vielfältige beschreibende Aufgaben sehr klar lesbar
lösen lassen: Isometrie, Dimetrie, Kavaliersperspektive
und Militärperspektive gehen zurück auf die Bemühungen barocker
Ingenierskunst, eindeutige Darstellungsverfahren für konstruktive
Aufgaben zu schaffen (Desargues "Brouillon project" 1636-40).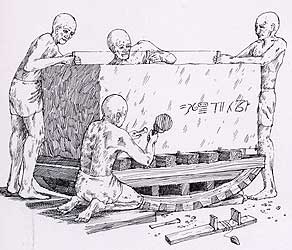
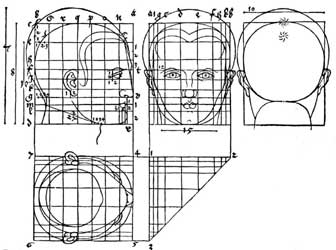


 Mit
einigem Erstaunen habe ich vor Jahren zur Kenntnis genommen, dass im Fach
Mathematik bereits in der Unterstufe des Gymnasiums Flächenberechnungen
an Quadern durchzuführen waren. Mein Erstaunen rührt daher, dass
ich aus dem Kunstunterricht noch in der Mittelstufe die Probleme kenne,
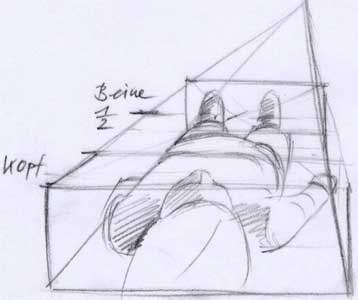
die Schüler mit der von Dürer übernommenen Aufgabe haben,
einen Kopf auf der Oberfläche eines Quaders abzuwickeln. Mund, Augen,
Nase in allen Ansichten auf die entsprechende Höhe und Breite zu projizieren,
das fällt im allgemeinen nicht leicht, was auch dem hier gezeigten
Beispiel zu entnehmen ist. Die Mehrzahl der Schüler dieser Altersstufe
antworten zwar richtig auf die Frage, welche Flächen in der Abwicklung
aneinandergrenzen, dennoch betrachten sie beim Zeichnen jede Teilansicht
für sich und führen Peilungen erst dann durch, wenn der Quader
zusammengeklebt ist.
Mit
einigem Erstaunen habe ich vor Jahren zur Kenntnis genommen, dass im Fach
Mathematik bereits in der Unterstufe des Gymnasiums Flächenberechnungen
an Quadern durchzuführen waren. Mein Erstaunen rührt daher, dass
ich aus dem Kunstunterricht noch in der Mittelstufe die Probleme kenne,
die Schüler mit der von Dürer übernommenen Aufgabe haben,
einen Kopf auf der Oberfläche eines Quaders abzuwickeln. Mund, Augen,
Nase in allen Ansichten auf die entsprechende Höhe und Breite zu projizieren,
das fällt im allgemeinen nicht leicht, was auch dem hier gezeigten
Beispiel zu entnehmen ist. Die Mehrzahl der Schüler dieser Altersstufe
antworten zwar richtig auf die Frage, welche Flächen in der Abwicklung
aneinandergrenzen, dennoch betrachten sie beim Zeichnen jede Teilansicht
für sich und führen Peilungen erst dann durch, wenn der Quader
zusammengeklebt ist.

 „Nach
allem, was man dort ablesen kann, können damals die Gesetzmäßigkeiten
der Perspektive in ihrem ganzen Umfang noch nicht begriffen gewesen sein.
Gleichwohl liegt es im Bereich der Wahrscheinlichkeit, dass es den antiken
Skenographen mit ihrem für visuell-optische Phänomene geschulten
Blick nicht entgangen ist, wie das sogenannte Fluchten von Parallelen,
ihr Zusammenstreben auf einen imaginären Punkt, dann nicht mehr wahrnehmbar
ist wenn die angeschauten Dinge in Bezug zur Größe des Betrachters
entweder sehr klein oder sehr weit entfernt sind, d.h. ihre Parallelen
auch im Bild annähernd parallel erscheinen müssen. Schaut man
z.B. eine Zündholzschachtel aus mehr als einem Meter Entfernung an,
so bleiben auch ihre Parallelkanten für die Wahrnehmung parallel,
ganz im Gegensatz zu denen eines Gebäudes aus >normaler Distanz<.
Theoretisch geht die Fluchtpunktperspektive bei einem unendlich großen
Abbildungsabstand, praktisch aber schon, wenn dieser ein erhebliches Vielfaches
der Gegenstandsgröße ausmacht, in die Parallelperspektive über,
in der eben Parallelität erhalten bleibt.“(Sellenriek
S. 58)
„Nach
allem, was man dort ablesen kann, können damals die Gesetzmäßigkeiten
der Perspektive in ihrem ganzen Umfang noch nicht begriffen gewesen sein.
Gleichwohl liegt es im Bereich der Wahrscheinlichkeit, dass es den antiken
Skenographen mit ihrem für visuell-optische Phänomene geschulten
Blick nicht entgangen ist, wie das sogenannte Fluchten von Parallelen,
ihr Zusammenstreben auf einen imaginären Punkt, dann nicht mehr wahrnehmbar
ist wenn die angeschauten Dinge in Bezug zur Größe des Betrachters
entweder sehr klein oder sehr weit entfernt sind, d.h. ihre Parallelen
auch im Bild annähernd parallel erscheinen müssen. Schaut man
z.B. eine Zündholzschachtel aus mehr als einem Meter Entfernung an,
so bleiben auch ihre Parallelkanten für die Wahrnehmung parallel,
ganz im Gegensatz zu denen eines Gebäudes aus >normaler Distanz<.
Theoretisch geht die Fluchtpunktperspektive bei einem unendlich großen
Abbildungsabstand, praktisch aber schon, wenn dieser ein erhebliches Vielfaches
der Gegenstandsgröße ausmacht, in die Parallelperspektive über,
in der eben Parallelität erhalten bleibt.“(Sellenriek
S. 58)

 „Wenn
man Häuser und größere Geräte auf einer Zeichenfläche
halbwegs erkennbar darstellen will, das heißt: ohne entweder etwas
Wesentliches wegzulassen oder ihren Zusammenhang zu verwirren, muß
man wohl oder übel die nach hinten verlaufenden Kanten durch schräge
Linien wiedergeben.“... „In der Kunst des fernen Ostens hat man tausend
Jahre lang die Tiefe durch schräg nach oben verlaufende Parallelen
angedeutet.“
„Wenn
man Häuser und größere Geräte auf einer Zeichenfläche
halbwegs erkennbar darstellen will, das heißt: ohne entweder etwas
Wesentliches wegzulassen oder ihren Zusammenhang zu verwirren, muß
man wohl oder übel die nach hinten verlaufenden Kanten durch schräge
Linien wiedergeben.“... „In der Kunst des fernen Ostens hat man tausend
Jahre lang die Tiefe durch schräg nach oben verlaufende Parallelen
angedeutet.“

 Die
Fluchtachse kommt vor allem dann als Konstruktionsprinzip in Frage, wenn
ein Innenraum als "Raumkasten"dargestellt werden soll. Bei Simone
Martini erfolgt das noch in einer Mischung aus parallelen und konvergierenden
Tiefenlinien.
Die
Fluchtachse kommt vor allem dann als Konstruktionsprinzip in Frage, wenn
ein Innenraum als "Raumkasten"dargestellt werden soll. Bei Simone
Martini erfolgt das noch in einer Mischung aus parallelen und konvergierenden
Tiefenlinien.
 Wenn
man Metzgers Argumentation betrachtet, so scheint er für die Schrägansicht
von „Häusern und größeren Geräten“ eine gewisse Notwendigkeit
zu sehen. Worin besteht aber diese Notwendigkeit, wo doch auch die Ägypter
Häuser, Tische, Stühle abbilden, jedoch in keinem mir bekannten
Fall auf eine Schrägansicht zurückgreifen?
Wenn
man Metzgers Argumentation betrachtet, so scheint er für die Schrägansicht
von „Häusern und größeren Geräten“ eine gewisse Notwendigkeit
zu sehen. Worin besteht aber diese Notwendigkeit, wo doch auch die Ägypter
Häuser, Tische, Stühle abbilden, jedoch in keinem mir bekannten
Fall auf eine Schrägansicht zurückgreifen?


 Genau
besehen ist die Zentralperspektive sowohl als geometrische Konstruktion,
wie auch als symbolische Form ein sehr komplexes Gebilde, das sowohl in
der Geschichte der Malerei als auch in der akademischen und kunstpädagogischen
Ausbildung heute mit höchst unterschiedlichem Tiefgang studiert wurde
und wird. Ich habe es oft erlebt, dass von Lehrern einem Bild der Kunstgeschichte
eine ‚raffinierte Perspektivkonstruktion‘ unterstellt wurde, ohne
dass man den Wiedersprüchen oder auch Fehlern der konkreten Komposition
nachgegangen wäre. Es ist ja nicht damit getan den Orthogonalenfluchtpunkt
oder einen Horizont im Bild zu verwenden. Fluchtpunkte und Verkürzungen
in Bildern führen auch nicht zwangsweise zu "erscheinungsrichtigen"
Abbildern, sondern oft zu Verzerrungen und verwirrenden Behauptungen, die
jedem Gesichtssinnerlebnis entgegenstehen aber „konstruktive Richtigkeit“
behaupten.
Genau
besehen ist die Zentralperspektive sowohl als geometrische Konstruktion,
wie auch als symbolische Form ein sehr komplexes Gebilde, das sowohl in
der Geschichte der Malerei als auch in der akademischen und kunstpädagogischen
Ausbildung heute mit höchst unterschiedlichem Tiefgang studiert wurde
und wird. Ich habe es oft erlebt, dass von Lehrern einem Bild der Kunstgeschichte
eine ‚raffinierte Perspektivkonstruktion‘ unterstellt wurde, ohne
dass man den Wiedersprüchen oder auch Fehlern der konkreten Komposition
nachgegangen wäre. Es ist ja nicht damit getan den Orthogonalenfluchtpunkt
oder einen Horizont im Bild zu verwenden. Fluchtpunkte und Verkürzungen
in Bildern führen auch nicht zwangsweise zu "erscheinungsrichtigen"
Abbildern, sondern oft zu Verzerrungen und verwirrenden Behauptungen, die
jedem Gesichtssinnerlebnis entgegenstehen aber „konstruktive Richtigkeit“
behaupten.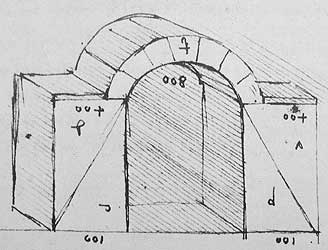
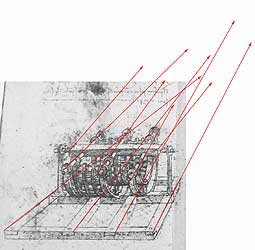 Viele
seiner Zeichnungen etwa aus dem Codex Madrid fertigte Leonardo freihand
entweder unter Verwendung eines Schrägbilds, das deutlich an eine
Kavaliersperspektive erinnert, oder im Bemühen um eine Fluchtpunktperspektive.
Ich finde es wenig verwunderlich, dass solchen Zeichnungen eine konstruktive
Stimmigkeit nachweislich abgeht. Ohne Lineal ist das Fluchten auf einen
Punkt, etwa bei einer starken Draufsicht, wenn die Fluchtlinien sehr lang
werden, nahezu unmöglich. Trotzdem wirkt die Darstellung auf den ersten
Blick nicht etwa unbeholfen oder unübersichtlich. Das führt mich
zu der Frage, warum überhaupt bei der Darstellung überschaubarer
Objekte eine zentrale Projektion sinnvoll sein kann. Meine Antwort: Wenn
die Tiefenausdehnung eines Objekts die von Höhe und Breite deutlich
übersteigt, beginnt die Parallelität von Orthogonalen merkwürdig
auszusehen. Oder: Wenn die Höhe eines Objekts die eigene Körpergröße
deutlich übersteigt, sollte eine Zeichnung nicht den Eindruck
erwecken, dass man auf die Bodenfläche in gleicher Weise Blicken kann,
wie auf die Deckfläche. Entsprechendes gilt für extrem breite
Objekte. Dann jeweils scheinen stürzende Linien eher angebracht als
parallele. Was aber sagt eine frontalperspektivische Konstruktion insgesamt
aus über die erscheinungsrichtige Verkürzung von Objekten?
Viele
seiner Zeichnungen etwa aus dem Codex Madrid fertigte Leonardo freihand
entweder unter Verwendung eines Schrägbilds, das deutlich an eine
Kavaliersperspektive erinnert, oder im Bemühen um eine Fluchtpunktperspektive.
Ich finde es wenig verwunderlich, dass solchen Zeichnungen eine konstruktive
Stimmigkeit nachweislich abgeht. Ohne Lineal ist das Fluchten auf einen
Punkt, etwa bei einer starken Draufsicht, wenn die Fluchtlinien sehr lang
werden, nahezu unmöglich. Trotzdem wirkt die Darstellung auf den ersten
Blick nicht etwa unbeholfen oder unübersichtlich. Das führt mich
zu der Frage, warum überhaupt bei der Darstellung überschaubarer
Objekte eine zentrale Projektion sinnvoll sein kann. Meine Antwort: Wenn
die Tiefenausdehnung eines Objekts die von Höhe und Breite deutlich
übersteigt, beginnt die Parallelität von Orthogonalen merkwürdig
auszusehen. Oder: Wenn die Höhe eines Objekts die eigene Körpergröße
deutlich übersteigt, sollte eine Zeichnung nicht den Eindruck
erwecken, dass man auf die Bodenfläche in gleicher Weise Blicken kann,
wie auf die Deckfläche. Entsprechendes gilt für extrem breite
Objekte. Dann jeweils scheinen stürzende Linien eher angebracht als
parallele. Was aber sagt eine frontalperspektivische Konstruktion insgesamt
aus über die erscheinungsrichtige Verkürzung von Objekten?

 Der
Abstand vom Objekt Würfel mit Kantenlänge 10 cm betrug bei der
linken Abbildung ca. 2m, bei einer Höhe von ca. 1m über der Tischplatte.
Die Kanten sehen in dieser Entfernung, Höhe und unter dem gegebenen
Objektwinkel nahezu parallel aus. Eine Konstruktion der Fluchtlinien über
einen Fluchtpunkt würde ein riesiges Blatt erfordern für ein
relativ kleines Bildobjekt. Beim rechten Bild lag der Abstand unter 1m
und die Aufnahme erfolgte etwa aus Augenhöhe in sitzender Position.
So etwa könnte ein Schüler im Unterricht vor einem derartigen
Objekt sitzen. Die Verkürzung wird erst dann deutlich, wenn die am
Tisch vorhandenen Linien beim Peilen zur Hilfe genommen werden. Ohne den
Vergleich mit dem Tisch ist das konvergieren der Tiefenlinien kaum zu beobachten.
Der Fluchtpunkt liegt immer noch so hoch, dass er vermutlich auf einem
Zeichenblatt nicht sinnvoll unterzubringen ist.
Der
Abstand vom Objekt Würfel mit Kantenlänge 10 cm betrug bei der
linken Abbildung ca. 2m, bei einer Höhe von ca. 1m über der Tischplatte.
Die Kanten sehen in dieser Entfernung, Höhe und unter dem gegebenen
Objektwinkel nahezu parallel aus. Eine Konstruktion der Fluchtlinien über
einen Fluchtpunkt würde ein riesiges Blatt erfordern für ein
relativ kleines Bildobjekt. Beim rechten Bild lag der Abstand unter 1m
und die Aufnahme erfolgte etwa aus Augenhöhe in sitzender Position.
So etwa könnte ein Schüler im Unterricht vor einem derartigen
Objekt sitzen. Die Verkürzung wird erst dann deutlich, wenn die am
Tisch vorhandenen Linien beim Peilen zur Hilfe genommen werden. Ohne den
Vergleich mit dem Tisch ist das konvergieren der Tiefenlinien kaum zu beobachten.
Der Fluchtpunkt liegt immer noch so hoch, dass er vermutlich auf einem
Zeichenblatt nicht sinnvoll unterzubringen ist.  Entfällt
die Orientierung etwa an den langen Linien eines Tisches, sieht die Sache
gleich anders aus und die Kanten eines Würfels erscheinen auch unter
diesem Blickwinkel nahezu parallel. Ich sehe darin eine hinreichende Argumentation
für die Forderung, etwa beim Sachzeichnen oder beim Zeichnen von Stilleben
im Unterricht auf eine konstruktive Ermittlung von Fluchtpunkten sowie
auf ein Konvergieren der Tiefenlinien zu verzichten. In den meisten Fällen
führt eine annähernd zeichnerische Paralellität der Tiefenlinien
zu einem angemessenen Erscheinungsbild. Die eigene Augenhöhe kann
eine Einschätzung liefern über die Flachheit von Deck- und Seitenfläche
des Körpers. Viel wesentlicher bei derartigen Studien ist das Abschätzen
der unterschiedlichen Raumrichtungen durch die Verdrehung der Seitenflächen
zueinander.
Entfällt
die Orientierung etwa an den langen Linien eines Tisches, sieht die Sache
gleich anders aus und die Kanten eines Würfels erscheinen auch unter
diesem Blickwinkel nahezu parallel. Ich sehe darin eine hinreichende Argumentation
für die Forderung, etwa beim Sachzeichnen oder beim Zeichnen von Stilleben
im Unterricht auf eine konstruktive Ermittlung von Fluchtpunkten sowie
auf ein Konvergieren der Tiefenlinien zu verzichten. In den meisten Fällen
führt eine annähernd zeichnerische Paralellität der Tiefenlinien
zu einem angemessenen Erscheinungsbild. Die eigene Augenhöhe kann
eine Einschätzung liefern über die Flachheit von Deck- und Seitenfläche
des Körpers. Viel wesentlicher bei derartigen Studien ist das Abschätzen
der unterschiedlichen Raumrichtungen durch die Verdrehung der Seitenflächen
zueinander.

 Ein
speziell
zum Problem der Verkürzung unternommener Versuch zeigt, wie wenig
überzeugend etwa auf 12-jährige ein fotografisches Argument wirken
kann; In einer Aufgabe sollten die Schüler einer 6. Jahrgangsstufe
anlässlich der Fußball Weltmeisterschaft die
Ein
speziell
zum Problem der Verkürzung unternommener Versuch zeigt, wie wenig
überzeugend etwa auf 12-jährige ein fotografisches Argument wirken
kann; In einer Aufgabe sollten die Schüler einer 6. Jahrgangsstufe
anlässlich der Fußball Weltmeisterschaft die 
 Ein
relativ einfacher Schritt, den schon 10-jährige nachvollziehen können,
ist das Fluchten von Linien, etwa von Bahngleisen auf einen Punkt.
Ein Begriff von Orthogonalen oder von der Bildebene ist dazu
noch nicht notwendig, und ist auch für diese Altersgruppe nicht sinnvoll.
Was Orthogonalen sind, sollte man erst in der Mittelstufe dann erläutern,
wenn man die 3-Ttafel-Projektion erklärt und in einfachen Anwendungen
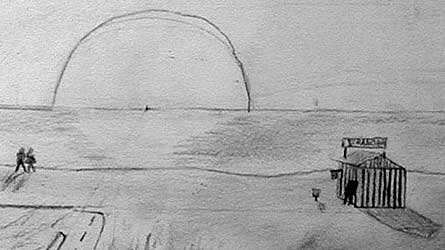
einübt. Die oben und im folgenden gezeigten Arbeiten stammen aus einer
6. Jahrgangsstufe zu einem so genannten „zentralperspektivischen Thema“.
Was der Schüler hier von den Erklärungen des Lehrers übernommen
hat, ist das Fluchten von Linien auf einen Horizont. Für diesen Schüler
blieb dieses Phänomen ein simples Zeichen, das mit seinen übrigen
Bildvorstellungen kaum in Einklang steht. Möglicherweise hat er den
mit dem Horizont vom Lehrer verknüpften Begriff von Unendlichkeit
mit einer Bildvorstellung vom Weltall assoziiert und ihn auf die Idee einer
Straße zum Mond gebracht. Nichts an diesem Bild deutet darauf hin,
dass er die Perspektive als ein Prinzip der Raumordnung begriffen
hat. Die gezeichneten Krater bilden nur eine sehr lose Systematik der Verkürzung.
Überschneidungen
werden bis auf li.vo. vermieden und die Horizontlinie dient ihm
noch als Standlinie für eine Reihe von Kratern. Die Straße
bleibt ein Fremdkörper in dieser Landschaft, etwa wie Stanley Kubricks
schwarzer Quader im Film 2001 – Odyssee im Weltraum.
Ein
relativ einfacher Schritt, den schon 10-jährige nachvollziehen können,
ist das Fluchten von Linien, etwa von Bahngleisen auf einen Punkt.
Ein Begriff von Orthogonalen oder von der Bildebene ist dazu
noch nicht notwendig, und ist auch für diese Altersgruppe nicht sinnvoll.
Was Orthogonalen sind, sollte man erst in der Mittelstufe dann erläutern,
wenn man die 3-Ttafel-Projektion erklärt und in einfachen Anwendungen
einübt. Die oben und im folgenden gezeigten Arbeiten stammen aus einer
6. Jahrgangsstufe zu einem so genannten „zentralperspektivischen Thema“.
Was der Schüler hier von den Erklärungen des Lehrers übernommen
hat, ist das Fluchten von Linien auf einen Horizont. Für diesen Schüler
blieb dieses Phänomen ein simples Zeichen, das mit seinen übrigen
Bildvorstellungen kaum in Einklang steht. Möglicherweise hat er den
mit dem Horizont vom Lehrer verknüpften Begriff von Unendlichkeit
mit einer Bildvorstellung vom Weltall assoziiert und ihn auf die Idee einer
Straße zum Mond gebracht. Nichts an diesem Bild deutet darauf hin,
dass er die Perspektive als ein Prinzip der Raumordnung begriffen
hat. Die gezeichneten Krater bilden nur eine sehr lose Systematik der Verkürzung.
Überschneidungen
werden bis auf li.vo. vermieden und die Horizontlinie dient ihm
noch als Standlinie für eine Reihe von Kratern. Die Straße
bleibt ein Fremdkörper in dieser Landschaft, etwa wie Stanley Kubricks
schwarzer Quader im Film 2001 – Odyssee im Weltraum.

 Etwas
schwerer zu vermitteln dürfte die Tatsache sein, dass es prinzipiell
für verschiedene Richtungen, die in die Tiefe führen, jeweils
eigene Fluchtpunkte gibt. In der Regel wird man die in den Raum führenden
Richtungen beschränken auf orthogonale Richtungen parallel zur Bodenebene.
Damit reduziert man die Möglichkeiten auf die sog. Frontalperspektive.
Bei Landschaftsbildern ergibt das eine eigenartige Komposition mit den
hier zu sehenden Stereotypen, die noch kein tieferes Verständnis der
Zentralprojektion voraussetzen: Der untere Bildrand spielt hier noch die
Rolle einer Standlinie für Mauer und Haus. Der Horizont
wird als zweite Standlinie eingeführt. Der Schüler ist von
der Unendlichkeit noch nicht ganz überzeugt, aber immerhin lässt
er den Blick des Betrachters am Horizont in einem Tunnel verschwinden.
Der Übergang vom kindlichen Standlinienbild zum Standlinienbild
mit Horizont ist dadurch symbolisiert, dass es eine Scheu davor gibt,
Dinge, die mit dem Boden verhaftet sind, in den Himmel hineinragen zu lassen.
Alles am Boden befindliche liegt unter dem Horizont, alles in der Luft
befindliche wird über dem Horizont abgebildet. Perspektivisch erzeugt
das einen Betrachter, dem kein Standpunkt auf dem Boden zuzuordnen ist.
Der Jugendliche hat noch nicht begriffen, dass sich im Fluchtpunkt der
Augpunkt abbildet. Gegenüber dem ersten Beispiel aus dieser Klasse
zeigt sich hier ein fortgeschrittener Ansatz für ein Verständnis
von perspektivischer Verkürzung: Die Bäume und Mittelstreifen
der Straße zeigen eine allmähliche Verkleinerung, allerdings
noch ohne jede visuelle Realistik. Die Zwischenräume, etwa bei den
Bäumen, bleiben weitgehend gleich, Überschneidungen im Sinn von
Staffelungen werden noch vermieden.
Etwas
schwerer zu vermitteln dürfte die Tatsache sein, dass es prinzipiell
für verschiedene Richtungen, die in die Tiefe führen, jeweils
eigene Fluchtpunkte gibt. In der Regel wird man die in den Raum führenden
Richtungen beschränken auf orthogonale Richtungen parallel zur Bodenebene.
Damit reduziert man die Möglichkeiten auf die sog. Frontalperspektive.
Bei Landschaftsbildern ergibt das eine eigenartige Komposition mit den
hier zu sehenden Stereotypen, die noch kein tieferes Verständnis der
Zentralprojektion voraussetzen: Der untere Bildrand spielt hier noch die
Rolle einer Standlinie für Mauer und Haus. Der Horizont
wird als zweite Standlinie eingeführt. Der Schüler ist von
der Unendlichkeit noch nicht ganz überzeugt, aber immerhin lässt
er den Blick des Betrachters am Horizont in einem Tunnel verschwinden.
Der Übergang vom kindlichen Standlinienbild zum Standlinienbild
mit Horizont ist dadurch symbolisiert, dass es eine Scheu davor gibt,
Dinge, die mit dem Boden verhaftet sind, in den Himmel hineinragen zu lassen.
Alles am Boden befindliche liegt unter dem Horizont, alles in der Luft
befindliche wird über dem Horizont abgebildet. Perspektivisch erzeugt
das einen Betrachter, dem kein Standpunkt auf dem Boden zuzuordnen ist.
Der Jugendliche hat noch nicht begriffen, dass sich im Fluchtpunkt der
Augpunkt abbildet. Gegenüber dem ersten Beispiel aus dieser Klasse
zeigt sich hier ein fortgeschrittener Ansatz für ein Verständnis
von perspektivischer Verkürzung: Die Bäume und Mittelstreifen
der Straße zeigen eine allmähliche Verkleinerung, allerdings
noch ohne jede visuelle Realistik. Die Zwischenräume, etwa bei den
Bäumen, bleiben weitgehend gleich, Überschneidungen im Sinn von
Staffelungen werden noch vermieden.

 Die
Einführung
eines Horizonts kann der gleichen Altersgruppe, in der viele Schüler
noch so zeichnen, wie nebenstehend links zu sehen ist, vermittelt werden
etwa als Grenze von Himmel und Erde. Ein Begriff von der Unendlichkeit
des perspektivischen Raums im Sinn von Grenzwertigkeit ist damit noch nicht
verbunden und wird sich den Kindern auch nicht erschließen.
Wenn sich Erdverbundenes über den Horizont erhebt, dann sind es häufig
Berge, die nicht etwa den Horizont überdecken, sondern ihn als
'Standlinie' benützen. In meinen Augen ist der Horizont als
Sichtgrenze der als eben definierten Bodenfläche erst für
die Oberstufe ein angemessener Stoff. Aber auch dafür ließen
sich Erkenntnispfade finden, etwa das Phänomen der Unschärfe
oder der Farbenperspektive.
Die
Einführung
eines Horizonts kann der gleichen Altersgruppe, in der viele Schüler
noch so zeichnen, wie nebenstehend links zu sehen ist, vermittelt werden
etwa als Grenze von Himmel und Erde. Ein Begriff von der Unendlichkeit
des perspektivischen Raums im Sinn von Grenzwertigkeit ist damit noch nicht
verbunden und wird sich den Kindern auch nicht erschließen.
Wenn sich Erdverbundenes über den Horizont erhebt, dann sind es häufig
Berge, die nicht etwa den Horizont überdecken, sondern ihn als
'Standlinie' benützen. In meinen Augen ist der Horizont als
Sichtgrenze der als eben definierten Bodenfläche erst für
die Oberstufe ein angemessener Stoff. Aber auch dafür ließen
sich Erkenntnispfade finden, etwa das Phänomen der Unschärfe
oder der Farbenperspektive.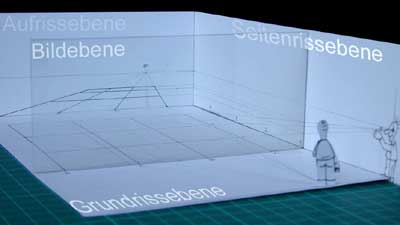 Die
erscheinungsrichtige Verkürzung der Sehdinge scheint mir eines der
schwierigeren Probleme der Zentralperspektive zu sein. Nach Panofsky scheint
die erste Veröffentlichung des Distanzpunktverfahrens erst Ende des
16. Jh, nämlich 1583 bei Vignola erfolgt zu sein. „Ob
das Distanzpunktverfahren in Italien vor Vignola-Danti bekannt war, ist
zumindest zweifelhaft.“(Panofsky, „Perspektive
als symbolische Form“ Anm.60) Damit bezweifelt Panofsky, dass Alberti,
Piero della Francesca, Leonardo, Dürer, um nur einmal die wichtigsten
Verbreiteter der Perspektivlehre zu nennen, die Distanz geometrisch exakt
bestimmt haben. Das Bildmotiv für alle Exerzitien der Verkürzung
des Tiefenraums ist der Plattenboden aus quadratischen Elementen. Alberti
führt die Quadratdiagonale als Regulativ für die stetige Verkürzung
ein. Der Diagonalfluchtpunkt scheint dann den nächsten Schritt
in der Entwicklung dargestellt zu haben. Ein realistischer Blick auf Architektur
etwa erfordert große Distanzen, was bei Zeichnungen in der Schule
unpraktisch wird, weil die Fluchtpunkte dann weit außerhalb des Zeichenblattes
liegen. Der Distanzpunkt setzt im Grunde eine Zusammenschau von Grundriss,
Seitenriss und Aufriss voraus, was für die Malerei einen erheblichen
praktischen Umstand darstellt wegen der Größe, die die Abwicklung
der 3-Tafel-Projektion selbst bei einer überschaubaren Bildgröße
erfordert. Nur so sind auch die Ratschläge zu verstehen, die in den
entsprechenden Lehrwerken für die Wahl des Diagonalwinkels gegeben
wurden. Schüler jedenfalls neigen dazu, beim Diagonalverfahren die
Verkürzung viel zu gering einzuschätzen, wodurch Projektionen
entstehen, die man direkt an die Nasenspitze halten müsste um einen
‚angemessenen‘ Eindruck von Verkürzung zu gewinnen. Populäre
Lehrbücher zur Perspektive verzichten auch heute noch auf eine Erklärung
der richtigen Distanz. Das „Handbuch der Zeichenkunst“ von José
M. Parramon 1989 z.B. empfiehlt für die Bemessung des ersten Abstands
eines Quadratischen Plattenbodens das ‚Augenmaß‘ heranzuziehen.
Der Rest erfolgt dann mechanisch über die Diagonalen der so abgegrenzten
Trapeze. „Perspektiven der Kunst“ von Nerdinger zeigt in Abb. 64 eine zentralperspektivische
Projektion eines Schachbrettmusters, gibt aber für die Verkürzung
keinen Hinweis auf die Distanzproblematik.
Die
erscheinungsrichtige Verkürzung der Sehdinge scheint mir eines der
schwierigeren Probleme der Zentralperspektive zu sein. Nach Panofsky scheint
die erste Veröffentlichung des Distanzpunktverfahrens erst Ende des
16. Jh, nämlich 1583 bei Vignola erfolgt zu sein. „Ob
das Distanzpunktverfahren in Italien vor Vignola-Danti bekannt war, ist
zumindest zweifelhaft.“(Panofsky, „Perspektive
als symbolische Form“ Anm.60) Damit bezweifelt Panofsky, dass Alberti,
Piero della Francesca, Leonardo, Dürer, um nur einmal die wichtigsten
Verbreiteter der Perspektivlehre zu nennen, die Distanz geometrisch exakt
bestimmt haben. Das Bildmotiv für alle Exerzitien der Verkürzung
des Tiefenraums ist der Plattenboden aus quadratischen Elementen. Alberti
führt die Quadratdiagonale als Regulativ für die stetige Verkürzung
ein. Der Diagonalfluchtpunkt scheint dann den nächsten Schritt
in der Entwicklung dargestellt zu haben. Ein realistischer Blick auf Architektur
etwa erfordert große Distanzen, was bei Zeichnungen in der Schule
unpraktisch wird, weil die Fluchtpunkte dann weit außerhalb des Zeichenblattes
liegen. Der Distanzpunkt setzt im Grunde eine Zusammenschau von Grundriss,
Seitenriss und Aufriss voraus, was für die Malerei einen erheblichen
praktischen Umstand darstellt wegen der Größe, die die Abwicklung
der 3-Tafel-Projektion selbst bei einer überschaubaren Bildgröße
erfordert. Nur so sind auch die Ratschläge zu verstehen, die in den
entsprechenden Lehrwerken für die Wahl des Diagonalwinkels gegeben
wurden. Schüler jedenfalls neigen dazu, beim Diagonalverfahren die
Verkürzung viel zu gering einzuschätzen, wodurch Projektionen
entstehen, die man direkt an die Nasenspitze halten müsste um einen
‚angemessenen‘ Eindruck von Verkürzung zu gewinnen. Populäre
Lehrbücher zur Perspektive verzichten auch heute noch auf eine Erklärung
der richtigen Distanz. Das „Handbuch der Zeichenkunst“ von José
M. Parramon 1989 z.B. empfiehlt für die Bemessung des ersten Abstands
eines Quadratischen Plattenbodens das ‚Augenmaß‘ heranzuziehen.
Der Rest erfolgt dann mechanisch über die Diagonalen der so abgegrenzten
Trapeze. „Perspektiven der Kunst“ von Nerdinger zeigt in Abb. 64 eine zentralperspektivische
Projektion eines Schachbrettmusters, gibt aber für die Verkürzung
keinen Hinweis auf die Distanzproblematik.